
Under Pressure
Experiment & Explore

| Ages | Cost | Time |
|---|---|---|
| 14+ | Medium | About 60 minutes |
What if I told you that I can crush a rock or lift a car with my just my finger? You might think I’m Superman. You would probably think I’m crazy! But it’s true, and you can too. That’s the power of science, engineering, and hydraulics.
In this Experiment and Explore activity, you will discover the awesome power of hydraulics and explore ways engineers put this to work to solve real-world problems.
You may want some towels on hand to clean up any leaks during this experiment!
You are going to conduct two separate but related experiments.
Experiment 1:
Connect the two 10 ml syringes (one with its plunger drawn out, the other pushed in) with the flexible tube. We will call the syringe with its plunger pulled out, A and the other syringe, B.

Next, disconnect the syringes so that syringe A still has the tube connected to
it. Fill syringe A and the tube with water. Push the plunger of syringe B all the
way in again and reconnect it to the tube.

For Experiment 1, you'll need the following materials.
You will also need the following items to do some additional investigations.
Experiment 2:
In this experiment we will swap out one of the 10 ml syringes with a 20 ml syringe. Disconnect the syringes so that one syringe still has the tube connected to it. Make sure this syringe and the tube are filled with water. Push the plunger of the 20 ml syringe all the way in and connect it to the tube.

A cross section is a thin slice across an object that lets you visualize the inside of that object or perform calculations. The shape of the object and the angle at which you take the slice determine the shape of the cross-section. Can you see that the cross-sectional area of the 20 ml syringe is larger than the 10 ml syringe?
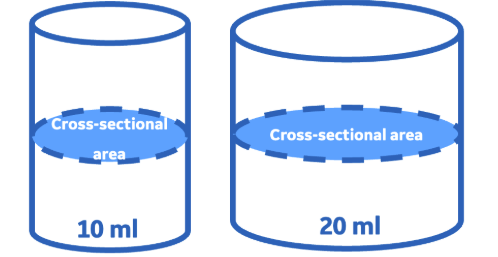
You can think of the cross-sectional area as the area of the shape that you would see after cutting an object into two pieces.
What's happening
In Experiment 1, we saw that if we pushed plunger A in, plunger B moved out when the syringes were filled with air (a gas) or water (a liquid). The force we applied to plunger A was transferred by the air or water to plunger B, making it move.
However, when we tried to stop plunger A from moving, when we pushed plunger B back in we discovered that the air in our syringes could be compressed or forced into a smaller volume (to a point). We were able to keep plunger A from moving quite easily. Most of the force we applied to push plunger B in went into compressing the air rather than moving plunger A out. In other words, very little force was transferred to plunger A.
But this was not the case when the syringes were filled with water. Water (like most other liquids) is incompressible. Very little of the force was ‘wasted’ on compressing the water, and almost all of it was transferred directly to plunger A from plunger B.
This phenomenon is called Pascal’s Principle (or Law). It states that in a confined incompressible fluid, (like water in a syringe) a pressure change in one part of the fluid is transmitted without loss to every other part of the fluid and to the walls of the container.
In Experiment 1, the syringes were the same size. In Experiment 2, they were different sizes. The 20 ml syringe had a larger cross-sectional area than the 10 ml syringe.
When we had two 10 ml syringes connected together, both syringes always moved the same distance and with the same force. However, when we connected a 20 ml syringe, we saw that the distance travelled by the 10 ml plunger was always greater than the distance travelled by the 20 ml plunger. This makes sense because the 20 ml syringe holds more water for each unit distance that the plunger moves.
We also discovered that it was much harder to stop the 20 ml plunger from moving than the 10 ml plunger. The force applied to the 10 ml plunger was multiplied at the 20 ml plunger.
It turns out that the force (F) applied to each plunger is related to the cross -sectional area (A) of the respective syringe as follows:
\[
\frac{\text{Cross-sectional area}_{10\,\text{ml}}}{\text{Cross-sectional area}_{20\,\text{ml}}} = \frac{\text{Force}_{10\,\text{ml}}}{\text{Force}_{20\,\text{ml}}}
\]
Or
\[
\frac{\text{Force}_{10\,\text{ml}}}{\text{Cross-sectional area}_{10\,\text{ml}}} = \frac{\text{Force}_{20\,\text{ml}}}{\text{Cross-sectional area}_{20\,\text{ml}}}
\]
This means that if we have two syringes, a green syringe (A) and an orange syringe (B), and if the cross-sectional area of syringe B is double that of syringe A, then the force applied to syringe B will also be double the force applied to syringe A. In other words, if you apply a force of 10 N at plunger A, we will get a force of 20 N applied at plunger B.
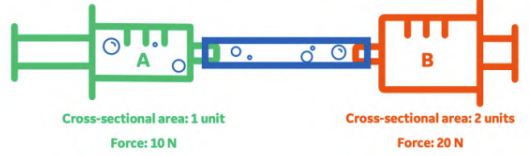
However, nothing is for free. What we gain in the force applied at plunger B is lost in the distance plunger B moves. If plunger A moves 10 cm, plunger B will only move half this distance, i.e., 5 cm.

We can express this mathematically as:
\[
\frac{\text{Cross-sectional area}_{10\,\text{ml}}}{\text{Cross-sectional area}_{20\,\text{ml}}} = \frac{\text{Distance}_{20\,\text{ml}}}{\text{Distance}_{10\,\text{ml}}}
\]
If the difference in the cross-sectional areas between two syringes or between any two cylinders with movable pistons is great enough, you can build a machine able to multiply the force you apply at the smaller piston (the input) that is great enough to crush a rock or lift a car at the bigger piston (the output). Such a system is called a hydraulic system.
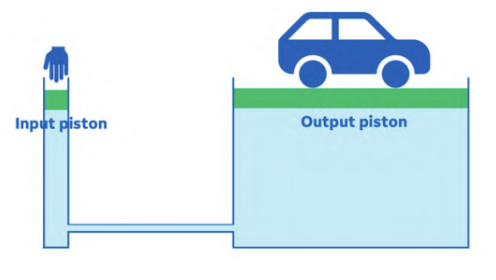
Watch the video called How a hydraulic jack works (3D Animation | Pascal Principle) (3:19) to see a simple explanation of hydrostatic pressure and how this can be applied to allow us to lift very heavy objects or crush things (sometimes just for fun - TOP 100 ITEMS UNDER HYDRAULIC PRESS (14:12)
Able to be forced or squeezed into a smaller space or volume, at least to a point. Gasses are compressible.
Unable to be forced or squeezed into a smaller space or volume. Most liquids and solids are incompressible.
In a confined incompressible fluid, a pressure change in one part of the fluid is transmitted without loss to every other part of the fluid and to the walls of the container.
The area of a 2D shape obtained by slicing through a 3D shape (like a cylinder) at a right angle.
We measure force applied (how hard something is pushed or pulled) in Newtons in honor of sir Isaac Newton. A force of 1 N is the force needed to lift up a 100 g bar of chocolate.
Hydraulic systems are all around you. They are used in cranes and earthmoving machines, car steering and brakes, robots, forklifts, elevators, and even bicycle brakes.
The diameter is the distance from one side of a circle to another through the center.
Watch these videos to learn even more about Hydraulic system and their uses.
Knowing what you now know about hydraulic systems and how to make one, try
these experiments yourself.
Use these measurements to calculate the cross-sectional area of the inside of each syringe. If you need help with this, use the online calculator at https://www.omnicalculator.com/math/area-of-a-circle. What is the ratio between the cross-sectional area of each syringe? Or, what is
\[
\frac{A_{\text{input}}}{A_{\text{output}}} = \frac{A_{10\,\text{ml}}}{A_{20\,\text{ml}}}
\]
In other words, if the cross-sectional area of the 10 ml syringe is 679 mm2 and the cross-sectional area of the 20 ml syringe is 1207 mm2, then the ratio would be
\[
\frac{A_{10\,\text{ml}}}{A_{20\,\text{ml}}} = \frac{679\,\text{mm}^2}{1207\,\text{mm}^2} = 0.56
\]
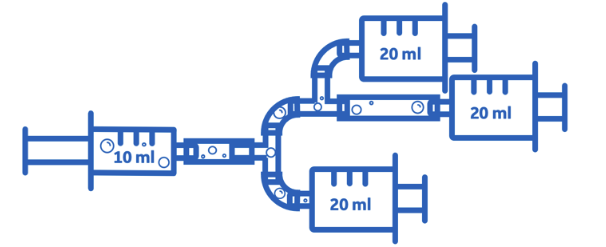
Now, use a t-piece hose connector to connect two 20 ml syringes (the output) to a single 10 ml syringe (the input) as shown below. As usual, make sure that the 10 ml syringe and all the tubes are full of water before connecting the 20 ml syringes and that the 20 ml plungers are pushed all the way in.
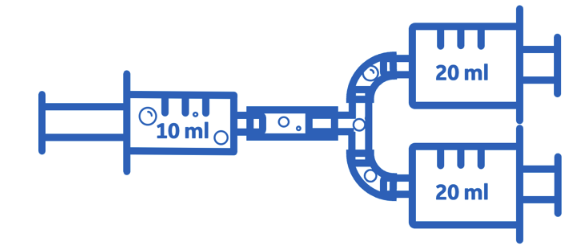
Add another t-piece to your setup so that you can connect three 20 ml syringes (the output) to one 10 ml syringe (the input).
Syringe hydraulic systems are fun to play with, but do you think we can use hydraulic systems to solve real-world problems? Consider these possibilities.
Share your ideas at #nextengineersdiy