The mathematical constant called pi (given the symbol π) has a value of about 3.14. This is only an approximate value because π is an irrational number. This means that it cannot be written as a fraction of two other numbers and that it has an infinite number of digits after the decimal place that never repeat in any sort of pattern.
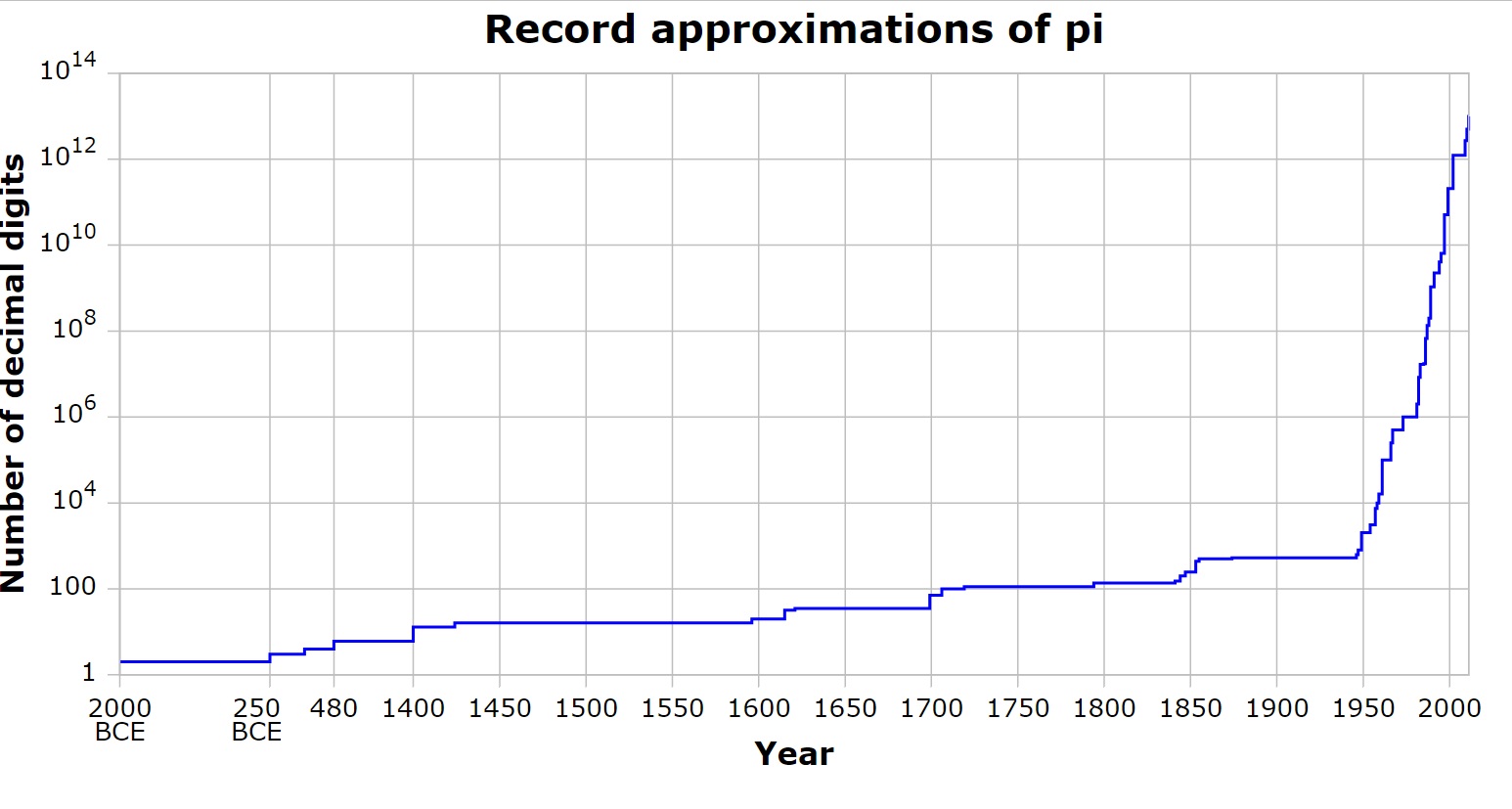
Calculating the value of π ever more accurately (i.e., finding more and more of its digits) has been something of an obsession for many mathematicians through the ages. Many different methods have been used with differing degrees of success. The table below lists some of the many highlights. A full list can be viewed at Chronology of computation of π.
|
Date |
Mathematician |
Correct decimal places |
|
2 000 BCE |
Ancient Egyptians and Babylonians |
1 |
|
250 BCE |
Archimedes |
2 |
|
150 |
Ptolemy |
3 |
|
480 |
Zu Chongzhi |
7 |
|
1400 |
Madhava of Sangamagrama |
10 |
|
1424 |
Jamshīd al-Kāshī |
16 |
|
1621 |
Willebrord Snell |
35 |
|
1630 |
Christoph Grienberger |
38 |
|
1706 |
John Machin |
100 |
|
1853 |
William Shanks |
527 |
|
1946 |
D. F. Ferguson |
620 (most ever by hand) |
|
1949 |
G. W. Reitwiesner |
2 037 (first use of a computer) |
|
2021 |
University of Applied Sciences of the Grisons |
62.8 trillion |
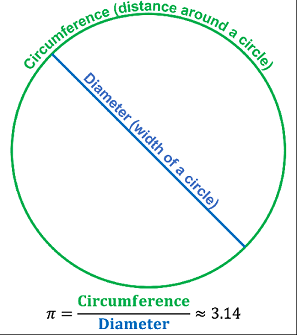
Pi (represented by the Greek letter π) is the ratio of the length of a circle’s circumference to its diameter and has a value of approximately 3.14.
Learn more about Pi in part 1 of this Nerd Out series.
The following graph illustrates the number of digits of π that have been correctly calculated over time. One can see that from 1950 and the advent of modern electronic computers, this has increased quickly.
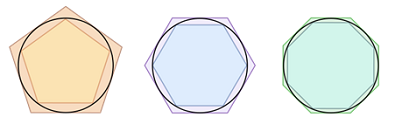
One of the most common methods throughout history of computing the digits of π has been the one devised by Archimedes. This method does not calculate the digits of π directly but rather defines lower and upper bounds for its value. The method is simple to understand but can be quite tricky to use.
It involves working out the perimeter of the inscribed polygon (the polygon drawn inside the circle) as the value of the lower bound and the perimeter of the circumscribed polygon (the polygon drawn around the circle) as the value of the upper bound. As we can see from the image below, the perimeter of the circle lies between these two bounds and the more sides the polygon has, the closer these bounds get to the actual circumference of the circle.
Watch the video called How did Archimedes Calculate Pi? (1:32) to see how he did it.
Note that Archimedes went as far as inscribing and circumscribing a 96-sided polygon. Try your hand at approximating the value of π with this simple simulation.
Is there a way of deriving formulae for the perimeter of the inscribed and circumscribed polygons based on their number of sides rather than calculating their perimeters from scratch each time?
Watch the video called How to Calculate Pi, Archimedes' Method (5:00) if you need help.
But this method can be very laborious and tedious. While under lockdown at home in 1666, Newton was bored and so started to fiddle with some mathematics. What resulted was an entirely new way to calculate the value of π. Learn more about his method by watching the video called The Discovery That Transformed Pi (18:39).
Then there are some other, less rigorous methods like the so-called Monte Carlo method, which relies on randomness to generate an approximate value of π. It is easy to do but does not always result in the most accurate approximations.
Cut out a square from a piece of cardboard and draw a circle within it. Now throw darts at the square and count how many holes you make inside and outside the circle. Use these values and the following formula to calculate an approximate value of π.
\[ \pi=4×\frac{\text{Holes inside the circle}}{\text{Total number of holes}} \]
See how to approximate the Monte Carlo method in action in this simulation.
The Monte-Carlo method uses randomness to generate an approximate value for π. Watch the video called Calculating Pi with Darts (5:47) to learn more.
How close can you get?
Above, we discussed three different methods for approximating the value of π but there are more, like the Buffon’s Needle method. Choose any method you like and do your own approximation of π. Share your process and results with the rest of the world using #NextEngineersDIY.