Are time machines real? Can we see back in time? As strange as it may seem, we see into the past all the time. Think about it like this. You are on a video call with a friend who lives in another country. They look into their camera and say “Hi”. The light bounces off their face and travels into the camera. This all takes time. Not much time, but some. About one billionth of a second. 

Next, their camera converts this light into electronic signals that are then sent by their computer to the Internet. This all takes time. Not much, but some. 

After some more time, these signals reach your computer where they are converted back into light by your screen. This light travels to your eyes where it is converted into signals that travel along your optic nerve to your brain. This all takes time. Not much, but some. 

It might seem like your conversation is instant, but every step takes time. Not much, but some. What you see happened in the past. To be fair, it is not the distant past, but it is still in the past. 

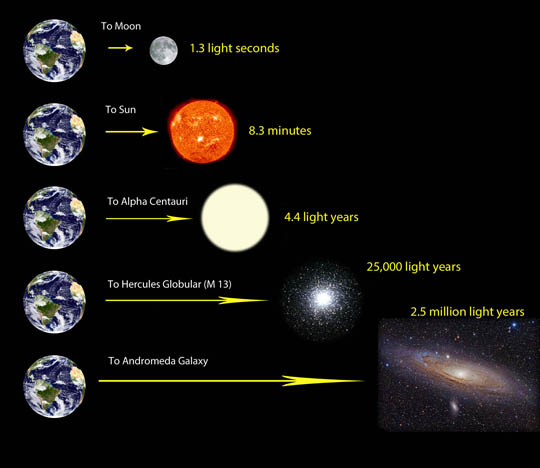
The same sort of time delay happens when light travels through space. Light is fast. It travels at just under 300 million meters per second or 1.08 billion km/h (671 million mph). But space is very big. For example, it takes light from the Sun over eight minutes to get to Earth. That beautiful sunset you saw? It happened eight minutes ago. 

The further away something in space is from us, the further the light has to travel and so the longer it takes to get to us. The nearest star to us, Proxima Centauri, is 4.24 light years away. We see this star as it was more than 4 years ago. The nearest major galaxy to us, the Andromeda galaxy, is 2.5 million light years away! The star-studded NGC 3972 galaxy is so far away (65 million light years) that the light we see started its journey around the time the dinosaurs went extinct.